国中数学｜菱形面积怎么算？一篇认识菱形定义、性质与常见题型

菱形是国中数学一定会学到的一种特殊四边形，学生需要认识不同的几何图形、辨认其特性从而推导数学公式，而在生活中随处都可以观察到的菱形的物品到底有哪些特性呢？以下小编将会逐一介绍菱形的基本定义、计算方式与试题范例，供各位读者做参考：

菱形的基本定义与性质

菱形的基本定义

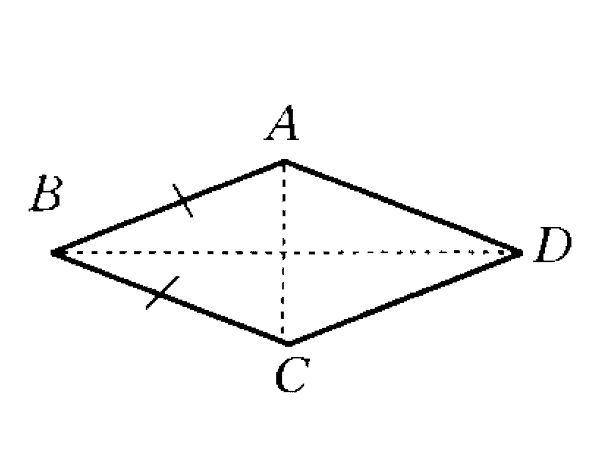
菱形Rhombus的定义为四边长度皆相等且对角线互相垂直平分，其对角线共有两条。

像是上图中，AB的距离=BC的距离＝CD的距离＝DA的距离，且中间两条对角线互相垂直平均分割。

菱形有哪些特殊性质？

菱形的特殊性质为：

四条边长都相等；

对角线互相垂直平分；

由中心点出发左右两侧均为对称。

菱形是平行四边形吗？

许多学生在刚接触菱形时会将其与平行四边形混淆，但其实两者并不绝对相同。平行四边形的性质为对边相等，而菱形的性质是四边等长，符合平行四边形的定义，因此菱菱形是平行四边形的一种，但平行四边形不一定就是菱形。

以下将整理了其他的特殊平行四边形，供各位读者做参考：

还有哪些特殊的平行四边形？

除了菱形之外，还有其他特殊的平行四边形如下：

长方形

长方形的定义为有一个角是直角，且四个边长互相平行的四边形。

正方形

正方形的定义为：四边均相等，且四个角都是直角的四边形。

梯形

梯形的定义为：只有一组对边互相平行，另一组不平行，且呈现一边凸起的四边形。

等腰梯形

等腰梯形的定义为：两侧边长度相等，且两底角度相等的梯形，更能被一条对称轴平分成两块相同大小的图形。

筝形

筝形的定义为：一条对角线可以垂直平分另一条对角线，且AB长度等于AD。

延伸阅读：秒懂梯形面积公式｜超详细解说＋例题演练，不用死背也能懂！

菱形面积怎么算？

图片来源：国中数学基本学习内容补救教材第四册

菱形的面积公式为：对角线乘积除以2，其推导方式是将平行四边形两条对角线画出，可以看到线条将菱形分成四块相同大小的直角三角形，将角AOD、角COD如上方图所示，移动到角BPA、角BQC的位置，因对角线互相垂直，在移动过后会形成一个长方形，可从而得知菱形ABCD 的面积=长方形APQC的面积，即：QC × AC 等于二分之一的BD × AC 也等于对角线乘积除以2

菱形定义、面积相关试题演练

1. 下列叙述何者错误？

（A）正方形是矩形

（B）正方形是菱形

（C）若四边形是矩形，则对角线互相垂直

（D）若四边形是菱形，则对角线互相平分

2.下图中菱形ABCD中，O为对角线AC、BC的交点，已知AC为8公分、BD为6公分，则菱形ABCD的周长为多少公分呢？

3.已知一菱形的对角线分别为8公分和12公分，则此菱形的面积为何？

4.将一张长方形的图画纸折叠两次（如下图），再剪去一个三角形，最后将图画纸展开，请问中间空心的形状为何种几何图形呢？